An Introduction to Formal Verification
subtitled "A non-introduction to my master thesis"
Lukas Prokop, 2016

Subtitled?
My master thesis is about
differential cryptanalysis with SAT solvers.
- I will not talk about differential cryptanalysis.
- I will talk a bit about SAT solvers.
→ ergo, this remains a "non-introduction".
→ However, I wrote the following library as first project for my master thesis.
Basics
Boolean Algebra
In mathematics and mathematical logic, Boolean algebra is the branch of algebra in which the values of the variables are the truth values true and false, usually denoted 1 and 0 respectively. […] the main operations of Boolean algebra are the conjunction and, denoted ∧, the disjunction or, denoted ∨, and the negation not, denoted ¬.
—Wikipedia:Boolean algebra
And, or, not
| AND | ||
| arg 1 | arg 2 | result |
| false | false | false |
| false | true | false |
| true | false | false |
| true | true | true |
Compare with tools:truthtable.
And, or, not
| OR | ||
| arg 1 | arg 2 | result |
| false | false | false |
| false | true | true |
| true | false | true |
| true | true | true |
Compare with tools:truthtable.
And, or, not
| NOT | ||
| arg 1 | result | |
| false | true | |
| true | false | |
Compare with tools:truthtable.
Theorem 1
You can represent any boolean function as combination of AND, OR and NOT.
Proof
It is a simple exercise to generate all 8 functions for 2 input bits and 1 output bit (22+1 = 8). Let k=2 be your induction base. Consider arguments Ak-1, one additional value b, result r and boolean function f. f(Vk) AND b = r or f(Vk) AND (NOT b) = r is an extension to f to k+1 arguments where x=y means ((NOT x) OR y) AND ((NOT y) or X)
Implication
| IMPLY | ||
| arg 1 | arg 2 | result |
| false | false | true |
| false | true | true |
| true | false | false |
| true | true | true |
Equality
| EQUALS | ||
| arg 1 | arg 2 | result |
| false | false | true |
| false | true | false |
| true | false | false |
| true | true | true |
Exclusive OR
| XOR | ||
| arg 1 | arg 2 | result |
| false | false | false |
| false | true | true |
| true | false | true |
| true | true | false |
And, or, not
| NAND | ||
| arg 1 | arg 2 | result |
| false | false | true |
| false | true | true |
| true | false | true |
| true | true | false |
Theorem 2
You can even represent any boolean function as combination of NANDs.
Proof
NOT x = (x NAND x)
(x AND y) = ((x NAND y) NAND (x NAND y))
(x OR y) = ((x NAND x) NAND (y NAND y))
What is boolean algebra good for?
Theorem 3
Every algorithm can be represented with AND, OR and NOT.
Proof
Proof is difficult, but our computer is built using transistors and stuff, right? And yes, I disregarded their physical properties. Sorry.
Our computer is a huge clusterf*ck of boolean algebra in action
Formal verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of intended algorithms underlying a system with respect to a certain formal specification or property, using formal methods of mathematics
—Wikipedia:Formal verification
Formal methods of mathematics?
Finite State Machines?
Petri nets?
Process algebra?
Hoare logic?
Yeah, possibly. But let's stick to boolean algebra.
Verification & Validation
- Validation
- Are we doing the right thing?
(do we meet user's needs?) - Verification
- Does the thing work correctly?
(does machine behavior match our intents?)
Addition of numbers
| arg 1 | 0 | 1 | 1 | 0 |
| arg 2 | 1 | 1 | 0 | 0 |
| arg 1+2 | ? | ? | ? | ? |
Addition of numbers
| arg 1 | 0 | 1 | 1 | 0 |
| arg 2 | 1 | 1 | 0 | 0 |
| arg 1+2 | ? | ? | ? | 0 |
Addition of numbers
| arg 1 | 0 | 1 | 1 | 0 |
| arg 2 | 1 | 1 | 0 | 0 |
| arg 1+2 | ? | ? | 1 | 0 |
Addition of numbers
| arg 1 | 0 | 1 | 1 | 0 |
| arg 2 | 1 | 1 | 0 | 0 |
| arg 1+2 | ? | 0 | 1 | 0 |
Addition of numbers
| arg 1 | 0 | 1 | 1 | 0 |
| arg 2 | 1 | 1 | 0 | 0 |
| arg 1+2 | 0 | 0 | 1 | 0 |
Example: Verification of addition
Given argument 3 and some value smaller 8,
expect result between 3 and 11.
Addition in boolean algebra
| a | 0 | 1 | 1 | 0 |
| b | 1 | 1 | 0 | 0 |
| c | 1 | 1 | 0 | 0 |
| r | 0 | 0 | 1 | 0 |
r0 = a0 XOR b0
c0 = a0 AND b0
Addition in boolean algebra
| a | 0 | 1 | 1 | 0 |
| b | 1 | 1 | 0 | 0 |
| c | 1 | 1 | 0 | 0 |
| r | 0 | 0 | 1 | 0 |
r1 = a1 XOR b1 XOR c0
c1 = (a1 AND b1) OR (b1 AND c0) OR (c0 AND a1)
Addition in boolean algebra
| a | 0 | 1 | 1 | 0 |
| b | 1 | 1 | 0 | 0 |
| c | 1 | 1 | 0 | 0 |
| r | 0 | 0 | 1 | 0 |
r2 = a2 XOR b2 XOR c1
c2 = (a2 AND b2) OR (b2 AND c1) OR (c1 AND a2)
Addition in boolean algebra
| a | 0 | 1 | 1 | 0 |
| b | 1 | 1 | 0 | 0 |
| c | 1 | 1 | 0 | 0 |
| r | 0 | 0 | 1 | 0 |
r3 = a3 XOR b3 XOR c2
c3 = (a3 AND b3) OR (b3 AND c2) OR (c2 AND a3)
Theorem 4
Every boolean function can be represented as ORs of ANDs of literals
Proof
-
Read line from truthtable and put AND between values. OR between lines.
XOR of a0, a1 and r as ANDs of ORs:
(¬a0 ∧ ¬a1 ∧ ¬r) ∨ (¬a0 ∧ a1 ∧ r) ∨
(a0 ∧ ¬a1 ∧ r) ∨ (a0 ∧ a1 ∧ ¬r)
Theorem 4
Every boolean function can be represented as ANDs of ORs of literals
Proof
- Read line from truthtable and AND values. OR lines.
- Negate the whole equation. OR becomes AND. AND becomes OR. Every value negates.
Previous XOR negated (and therefore ANDs of ORs):
(a0 ∨ a1 ∨ r) ∧ (a0 ∨ ¬a1 ∨ ¬r) ∧
(¬a0 ∨ a1 ∨ ¬r) ∧ (¬a0 ∨ ¬a1 ∨ r)
Terminology
- Literal
- a boolean variable, optionally with a sign
- Model
- a boolean assignment making the equation true
- Disjunctive Normal Form
- ORs of ANDs of literals
- Conjunctive Normal Form
- ANDs of ORs of literals
Satisfiability
A boolean function is satisfiable iff there exists some boolean assignment for variables such that the equation evaluates to true.
Satisfiability in 15 lines
#!/usr/bin/env python3 import inspect import itertools def f(a, b): return not a or b and not b argc = len(inspect.getargspec(f).args) for args in itertools.product([True, False], repeat=argc): if f(*args): print("SAT") break else: print("UNSAT")
Satisfiability runtime
| 2 arguments | <1 sec. |
|---|---|
| 4 arguments | ? sec. |
| 8 arguments | ? sec. |
| 16 arguments | ? sec. |
| 32 arguments | ? sec. |
… for an UNSAT function
with CPython 3.4.3
Satisfiability runtime
| 2 arguments | <1 sec. |
|---|---|
| 4 arguments | <1 sec. |
| 8 arguments | <1 sec. |
| 16 arguments | <1 sec. |
| 32 arguments | ? sec. |
… for an UNSAT function
Satisfiability runtime
| 20 arguments | <1 sec. |
|---|---|
| 21 arguments | 1.3 sec. |
| 22 arguments | 2.6 sec. |
| 23 arguments | 5.1 sec. |
| 24 arguments | 10.8 sec. |
| 25 arguments | 22.4 sec. |
| 26 arguments | 40 sec. |
… for an UNSAT function
Satisfiability runtime
| 20 arguments | 0.2 sec. |
|---|---|
| 21 arguments | 0.4 sec. |
| 22 arguments | 0.6 sec. |
| 23 arguments | 1.2 sec. |
| 24 arguments | 2.2 sec. |
| 25 arguments | 4.6 sec. |
| 26 arguments | 8.7 sec. |
… for an UNSAT function
with PyPy 2.5.0 compiled with GCC 4.9.2
Satisfiability runtime
Interpolation tells us that it will take 22 minutes to test one single 32-bit integer. It takes 66810602 days to test two 32-bit integers.
O(2n) for n variables.
Satisfiability runtime
But wait… this was the worst case and in python.
What about:
- trying to reach best case by analyzing the function?
- and using ASM/C/C++?
→ this is what SAT solvers typically do.
SAT competition
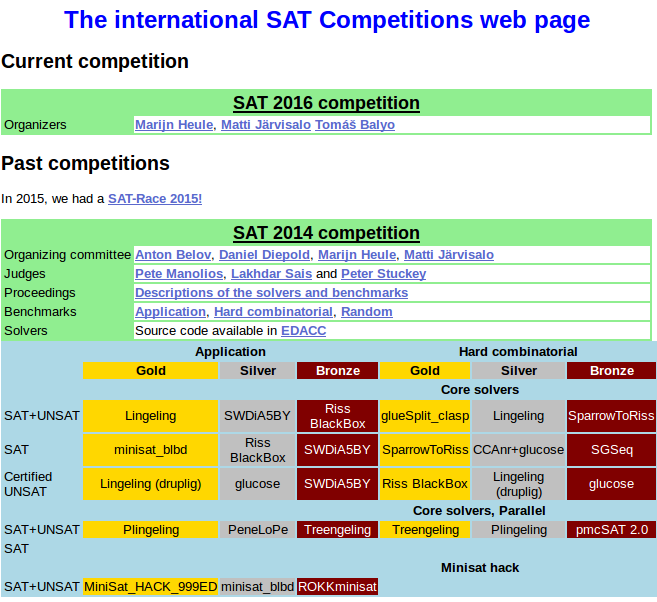
Back to Formal verification
A boolean function is satisfiable iff there exists some boolean assignment for variables such that the equation evaluates to true.
… becomes …
A boolean function is satisfiable iff an algorithm meets its specification.
algotocnf
Simple example
import algotocnf def algo(): a = 0x25 b = 0xFF return a ^ b def main(): env = algotocnf.evaluate() env.output(algo(), name='o') env.expect_output({'o': '0xDA'}) assert env.test(), "this input/output relation is not possible" print('Finished successfully.') if __name__ == '__main__': main()
More advanced example
#!/usr/bin/env python3 import io import algotocnf algo = lambda a, b: (a + b, a + b + 0x2) def main(): env = algotocnf.evaluate() env.solver_config.max_models = 5 # input is one of # {'x': '0b0100', 'y': '0b1010101'}, # {'x': '0b0101', 'y': '0b1010101'}, # {'x': '0b0110', 'y': '0b1010101'}, # {'x': '0b0111', 'y': '0b1010101'} x = env.input(bits='01??', name='x') y = env.input(constant=0x9, size=4, name='y') o1, o2 = algo(x, y)
More advanced example (cont.)
env.output(o1, name='o1')
env.output(o2, name='o2')
env.expect_output(
{'o1': '0b1101', 'o2': '0b1111'},
{'o1': '0b1110', 'o2': '0b0000'},
{'o1': '0b1111', 'o2': '0b0001'},
{'o1': '0b0000', 'o2': '0b0010'}
)
assert env.test(), "this input/output relation is not possible"
print('Finished successfully.')
if __name__ == '__main__':
main()
MD4 example
def main(): env = algotocnf.evaluate() env.solver_config.max_models = 10 md4 = MD4(env) # compute rounds = md4.update([0b10000000] + [0] * 15) # actual output for i, (a, b, c, d) in enumerate(rounds): env.output(b, name='B' + str(i)) # expected output after 1 round expectation = {} for i in range(48): expectation['B' + str(i)] = md4_trace[i] env.expect_output(expectation) assert env.test(), "this input/output relation is not possible" print('Finished successfully.')
algotocnf features
- dump CNF to file system, solve externally, inject solution
- differential values
- I claim: source code easy to adapt 😋
Behind the scenes
c Lingeling SAT Solver c c Version ats1o0 cfbdebf2806fb8a4b5b9d366561d56a57c2b9470 c c Copyright (C) 2010-2013 Armin Biere JKU Linz Austria. c All rights reserved. c c released Mon Apr 4 12:21:28 CEST 2016 c compiled Mon Apr 4 12:36:57 CEST 2016 c c gcc (Debian 4.9.2-10) 4.9.2 c -Wall -O3 -DNDBLSCR -DNLGLOG -DNDEBUG -DNCHKSOL -DNLGLPICOSAT c Linux cm 3.16.0-4-amd64 x86_64 c c reading input file algotocnf_21-t9_diff-desc_ocnf_s=21.cnf c no embedded options c found 'p cnf 146368 693512' header c read 146368 variables, 693512 clauses, 2344824 literals in 0.0 seconds
Behind the scenes
c c 581.268 18% analysis c 81.040 3% bump … c 0.000 0% phase c 0.000 0% rdp c ---------------------------------- c 2.464 0% probe simple 48% c 1.496 0% probe basic 29% c 1.216 0% probe tree-look 23% c ================================== c 1.540 0% preprocessing 1% c 132.340 4% inprocessing 99% c ================================== c 133.880 4% simplifying c 3087.696 96% search c ================================== c 3221.580 100% all c c 22244136 decisions, 6904.7 decisions/sec c 11915604 conflicts, 3698.7 conflicts/sec c 966541398 propagations, 0.3 megaprops/sec c 3221.6 seconds, 163.1 MB
Behind the scenes
s SATISFIABLE v -1 2 -3 4 5 -6 7 -8 9 -10 -11 -12 -13 -14 15 -16 -17 18 19 20 21 -22 -23 24 25 v -26 -27 28 29 -30 -31 32 -33 34 -35 36 37 -38 39 -40 41 -42 -43 -44 -45 -46 47 v -48 -49 50 51 52 53 -54 -55 56 57 -58 -59 60 61 -62 -63 64 -65 -66 -67 -68 -69 v -70 -71 -72 -73 -74 -75 -76 -77 -78 -79 -80 -81 -82 -83 -84 -85 -86 -87 -88 …
Every boolean variable represents one bit.
? becomes 0 or 1.
Complexity as a science
Wait… you just showed me some integer examples.
But I want everything™
Complexity as a science
The more you want…
the more you need to check …
the slower you are.
Tweet about Microsoft's Z3
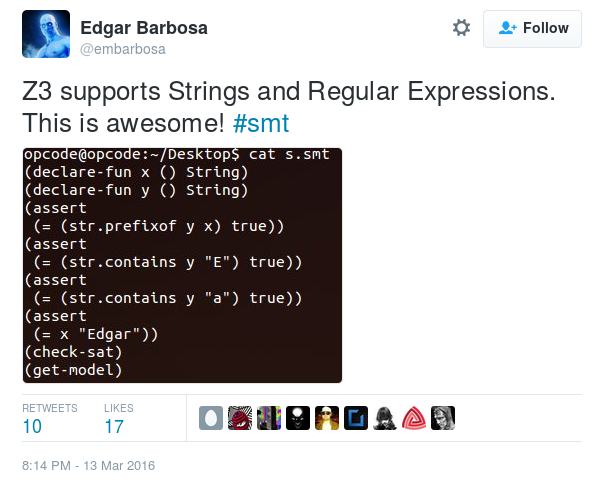
Complexity as a science
Distinction between problems becomes important.
Encoding becomes important
(which guarantees are encoded implicitly/explicitly?)
Strongly related:
- Temporal issues
- Constraint programming
- Equivalence of circuits
- Rewrite problem to a simpler one
Complexity as a science
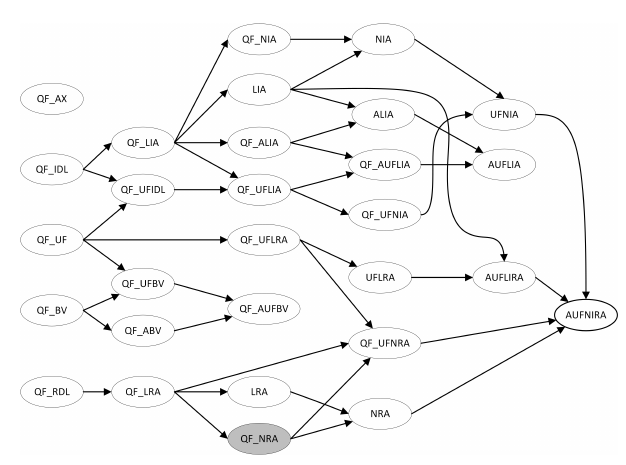
Complexity as a science
My library is just one of many. Like STP or boolector.
But it addresses specifically the issues I had during my master thesis (differential encoding, flexible encoding, export of CNF and solving it on a cluster). python was the easiest to use (no concurrency required, performance-critical part is limited to SAT solver).
Thank you
It was a pleasure to work in that field and with those tools. Thanks to all involved. You are mentioned in my thesis' Acknowledgements.
Thanks, pygraz for 4 years
… so far?!