Motivation
I originally planned to create a talk about post-quantum cryptography. Currently I cannot see this happening. Thus, I want to publish my drawings I created for the different categories of post-quantum cryptography.
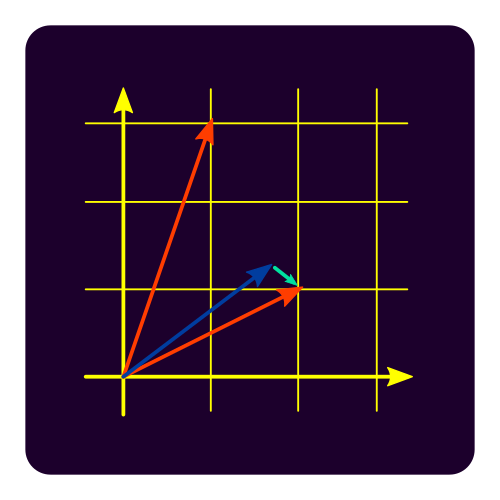
Lattice-based cryptography
Lattices are discrete subgroups of finite dimensional Euclidean vector spaces. As such the additive structure of vectors is used as graphical element. Finalists in round 3 are {NTRU, CRYSTALS-Kyber, Saber, CRYSTALS-Dilithium, FALCON}. Alternate NTRU Prime “simplifies” candidate NTRU and Frodo KEM provides a signature scheme. Source SVG.
Multivariate cryptography
Multivariate cryptography uses multivariate equations as mathematical objects. Schemes are built around the idea of the unbalanced oil and vinegar (UOV) scheme of Patarin. As such oil and vinegar are used as graphical elements. Rainbow is the only multivariate finalist in round 3, but signature scheme GeMSS is an alternate. Source SVG.

Hash-based cryptography
Hash-based cryptography is built around the idea of hash functions to generate trees of signatures. The basics are explained in a blogpost by David Wong. All round 3 candidates (Picnic, SPHINCS+) are only alternate candidates and only provide signature schemes. Hashes is either a dish or a mathematical map of variadic bits to fixed-length bits. As a result, I generated two versions. Sources are dish SVG and map SVG.

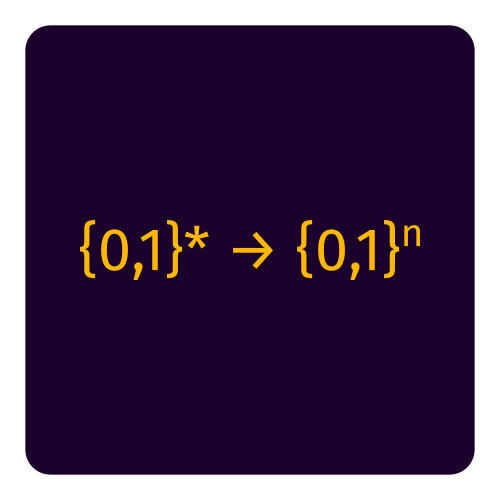
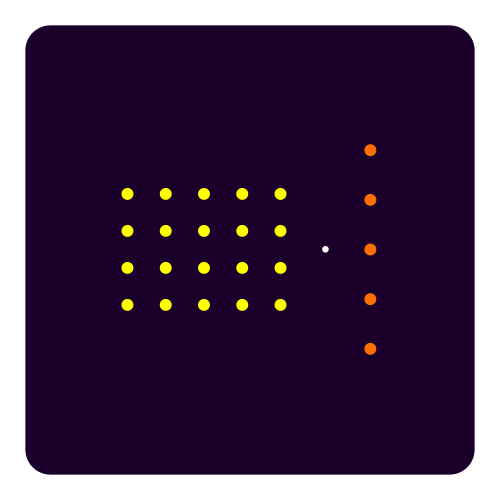
Code-based cryptography
Code-based cryptography are based on the idea of linear codes. A decoder removes an error introduced in the encryption process. Classic McEliece is the only round 3 finalist and works with binary Goppa codes whereas BIKE and HQC are alternates. The graphical elements are multiplication with a generator matrix on the one hand but also a pun source code on the other hand. Sources are mul SVG and src code SVG.

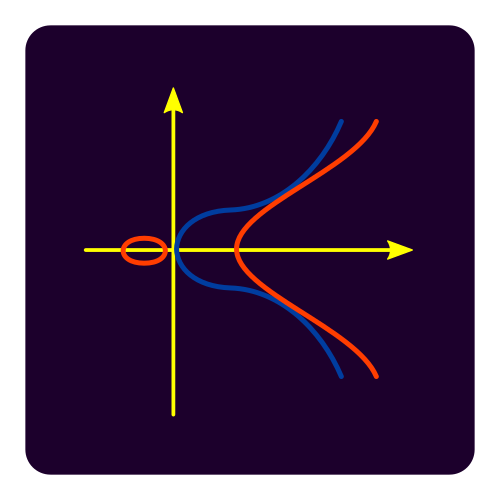
Supersingular elliptic curve isogeny cryptography
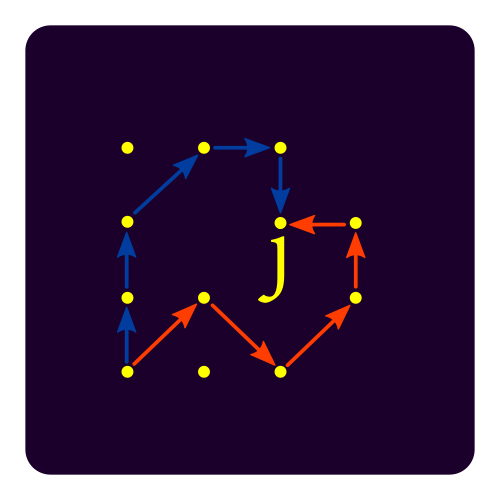
Isogenies are maps between elliptic curves. Since elliptic curves are well-studied mathematical objects, this field has a strong formal background. On the one hand, it provides very short signatures and a Diffie-Hellman-like scheme with forward secrecy, on the other hand it has performance issues. Round 3 alternate SIKE is the one representative. The graphical elements are elliptic curves in ℝn, but also the idea of walks along isomorphisms to end up at the same elliptic curve with the same j-invariant. Sources are elliptic SVG and walk SVG.
Conclusion
All files are published in the Public Domain. I hope you can use them in a meaningful way.