Graph-theoretic considerations for 'text documents as trees'

✍️ Written on 2022-12-18 in 3256 words.
Part of project typho digital-typesetting

Update 2023-01: I published this post too early. You can see the fixed version.

Motivation

The ‘texts documents as trees’ assumption is old. Most text document syntaxes have an inherent hierarchical structure and can thus be represented as tree. LISP does not hide this fact in its syntax. You can also see the importance of this notion from the Document Object Model (DOM) in HTML. XML trees is another keyword.

Today, I want to look at this topic from a graph theoretic point of view and establish four definitions for typesetting. Then we encode it in rust.

Text documents as trees

Text documents are used to encode information. For example, one can create a file with the following text.

Colorless green ideas sleep furiously — Noam Chomsky

One frequent requirement is that semantically distinct elements should be separated from each other. The quote is semantically distinct from its author. One can argue that the em-dash “—” separates the quote from its author. So we have one document with two elements (quote, author).

Because these distinctions are so frequent, syntaxes were invented which allow to encode generic semantic distinctions. One such an example is XML (eXtensible Markup Language). In XML, the previous example could be encoded like this:

<?xml version="1.0" encoding="utf-8"?>
<document>
  <quote>Colorless green ideas sleep furiously</quote>
  <author>Noam Chomsky</author>
</document>

The first line can be considered as constant, necessary text. Then for every name N, we can introduce syntactic elements <N> and </N> to start and end elements respectively. This is the synactic idea of XML. Another syntax is offered by the programming language LISP. In this case, the representation could look like this:

(document
  (quote "Colorless green ideas sleep furiously")
  (author "Noam Chomsky"))

In this case, parentheses are used to create a semantic element. And the first word denotes the semantic name. Since “document” wraps the two elements “quote” and “author”, it encodes the same structure with one root element and two childen. These two examples show how text documents can encode information together with semantic distinction through structure.

But one point needs to be mentioned explicitly: Structures are recursive meaning “inside an element, an element can occur”. We can see this in the XML case as well as the LISP case. This is not necessary, but a frequent pattern among text document syntaxes.

And if we put elements inside elements, we create a structure which is called tree.

Graphic theoretic definitions

A graph is a tuple of vertices and edges. For examples, vertices can be the set {1, 2, 3}. Here three vertices are represented as numbers. Edges are tuples which define which vertices are connected. For example, {(1, 2), (1, 3)} denotes that there is a connection between vertex #1 and #2 as well as vertex #1 and #3. The tuple ({1, 2, 3}, {(1, 2), {1, 3}}) is an example of a graph.

An undirected graph is given if the edge (1, 3) denotes a connection from vertex #1 to #3 as well as a connection from vertex #3 to #1. If only one direction is defined, the graph is called directed.

An undirected graph is connected if we find a connection between any pair of vertices. In the previous example, the pair {1, 2} is connected, because an edge (1, 2) connects it. Also the pair {2, 3} is connected, because we can go from #2 to #1 and from #1 to #3. We use both edges to reach our target. Since this holds true for any pair of vertices, the graph is connected.

A graph is called acyclic if no vertex has a connection to itself. Specifically, we need a non-empty sequence of edges starting and ending at the same vertex without using any intermediate vertex twice. In our example, let us start at vertex #2. We can reach #1 with the edge (1, 2). We can then reach vertex #3 with the edge (1, 3). But to get back from vertex #3 to #1, we would have to use vertex #2 again (no other edges connect them). Thus, vertex #2 has no connection to itself. In our example, this is true for all vertices and thus our example graph is acyclic.

A Tree is a connected acyclic undirected graph. It basically sums up the properties we just defined.

If we declare a specific vertex as root, we have a rooted tree. The definition of a root vertex does not require any additional constraints.

Visualizing trees is intuitive. Considering a rooted tree, we tend to put the root vertex at the top and horizontally align all vertices at the same level. What do I mean by level? The notion of levels can be defined by distance from the root. The root has distance 0 to itself (level 0), but all adjacent vertices are at level 1. These levels also constitute the notion of a hierarchy.

A picture showing a tree with three vertices and its hierarchy established by the distance from the root
Figure 1. Rooted tree with its hierarchy over two levels

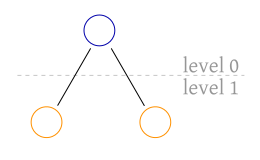
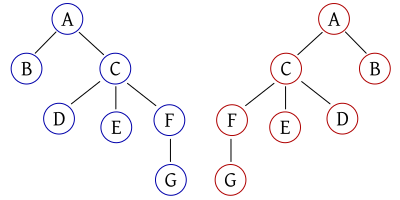
A tree is ordered, if the order of adjacent vertices is significant (TAOCP, volume 1, page 308). In the following image, we can see two different ordered trees, because their order is different. If the tree would be unordered, the trees would be the same.

A picture showing two trees with (for example) one tree showing root A with children B and C where the other tree shows root A with children C and B
Figure 2. Ordered trees differ in the sequential occurence of children

A colored tree is any tree with a color associated to each vertex. Often colors come with designated semantics (c.f. Red-black trees).

Encoding information in trees

So, we looked at some text document examples. We also established graph theoretic definitions. Now let us look how they fit together.

<?xml version="1.0" encoding="utf-8"?>
<document>
  <quote>Colorless green ideas sleep furiously</quote>
  <author>Noam Chomsky</author>
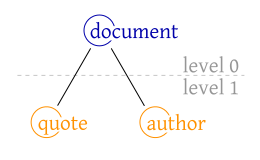
</document>

In the simplest manner, this document can be considered as tree which three vertices and two edges. The root vertex (corresponding to document) has an edge to vertex quote and author each. But in this model, we only have three vertices and vertices neither have names nor text like “Noam Chomsky”. As a result, we know that the text document leads to the following visualization, but many documents correspond to it because we lose information.

A picture showing a tree with three vertices distributed over two hierarchical levels
Figure 3. Rooted tree corresponding to our text document

Thus it is an immediate idea to annotate each vertex with an element name.

A picture showing a tree with vertices ‘document’
Figure 4. Rooted tree with element name annotations corresponding to our text document

Besides the element name, we can annotate additional information per vertex. To describe the layout of the information, we use the usual notions of data structures. For this we look at actual text document syntaxes in detail. I also think theses syntaxes are representative, because text documents commonly encode a subset of this information.

Text documents syntaxes in detail

In this section, we want to add the compiler construction perspective on trees. As such, when we use the words “node” and “vertex” synonymously.

LISP and S-expressions

LISP is a set of programming languages based on the idea of S-expressions (e.g. Scheme, Common LISP, Clojure, but partially also protocols like IMAP). S-expression where originally defined as expressions of the form …

(x . y)

where x and y denote expressions themselves or any atom (an atom is an element from the infinite set of distinguishable atomic elements, commonly any alphanumeric identifier). For example (concat . 4 . (3 . NIL . (2 . NIL))) could denote the concatenation of the lists [4, 3] and [2]. But this notation of S-expressions is rather archaic. A more modern syntax would be (concat (list 4 3) (list 2)). Here the expressions are variadic, not necessarily binary w.r.t. arguments and the list command allows to skip NIL (= not-in-list) declarations. Semantics of commands like concat and list are outside the scope of S-expressions (but subject to the dialect like Scheme/Clojure). S-expressions are syntactic concepts which make the hierarchical structure very explicit.

Consider the following Scheme expressions:

(define square (lambda (x) (* x x)))
(square (square 2))

Then its expression tree can be visualized the following way:

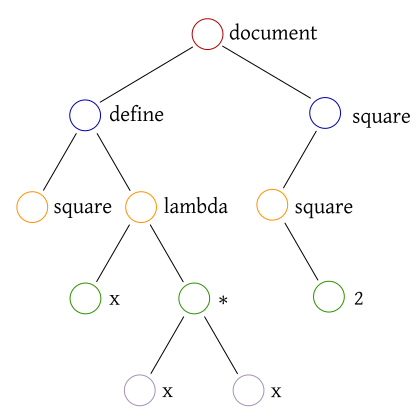
Rooted tree representing the LISP expressions above
Figure 5. Rooted tree corresponding to the LISP expressions

In order to model the contained data, we observe the following properties:

  • We introduced a root node “document”, not found in the LISP text document. This is desirable because one node should encompass the entire content.

  • Each pair of parentheses define a node where the first contained word gives the element name.

XML trees

XML is another syntactic concept which makes its tree structure very explicit. XML notation is based on SGML, but uses a more consistent syntax to simplify error handling. The example above could be denoted as:

<?xml version="1.0"?>
<document>
  <command name="define">
    <atom>square</atom>
    <command name="lambda">
      <command name="x"/>
      <command name="*">
        <atom>x</atom>
        <atom>x</atom>
      </command>
    </command>
  </command>
  <command name="square">
    <command name="square">
      <atom>2</atom>
    </command>
  </command>
</document>

Here, we see certain differences between XML and LISP:

  • Unlike LISP, XML requires one top-level element. So we can see our root element <document/> explicitly in XML.

  • Furthermore the set of names for LISP commands and XML elements differ. I introduced <command/> elements with a so-called attribute name. I had to introduce this name attribute because * is not a permitted name for XML elements but as attribute value. For LISP, the set of commands is not defined but a dialect like Scheme indeed permits * as command.

Summarizing discussion

In conclusion, we observed the following properties:

  • One root element is desirable. If it is not in the source document, we create one.

  • Each element name must be non-empty but might contain various whitespace-free characters in its name.

  • Each element might have associated attributes which is a map of strings to strings.

  • Elements wrap elements and thus create a hierarchy.

Four definitions for typesetting

Now the question arises: which data model makes sense to abstract these document strutures? I claim for digital typesetting, we want to distinguish four kinds:

Structure tree

rooted, ordered tree with a non-empty whitespace-free name per node

Content tree

rooted, ordered tree with a non-empty whitespace-free name and attributes associating strings to strings per node

XML tree

A rooted, ordered, colored tree. Green nodes have a non-empty whitespace-free name and attributes associating strings to strings. Blue nodes do not have a name but just a string as text. Green nodes have ordered children vertices whereas blue nodes cannot have such.

Attribute-node tree

A rooted, ordered, colored tree. Green nodes have a non-empty whitespace-free name and attributes associating strings to nodes. Blue nodes do not have a name but just a string as text. Green nodes have ordered children vertices whereas blue nodes cannot have such.

Structure trees are powerless, because they can only carry information about the structure of the document. Content tree can carry text, because one could store the information inside the attributes. But XML trees move the conventional storage of text inside attributes into its blue nodes. Finally, attribute-node trees are more powerful because attribute values can have trees themselves.

rust representation of data structures

In the following, I would like to provide these definitions also as data structures in rust:

pub struct Node {
  pub element: String,
  pub children: Vec<Box<Node>>,
}

pub type StructureTree = Node;
pub struct Node {
  pub element: String,
  pub attrs: HashMap<String, String>,
  pub children: Vec<Box<Node>>,
}

pub type ContentTree = Node;
pub struct ElementNode {
    pub name: String,
    pub attrs: HashMap<String, String>,
    pub content: Vec<Node>,
}

pub enum Node {
    Element(ElementNode),
    Text(String),
}

pub type XMLTree = ElementNode;
pub struct ElementNode {
    pub name: String,
    pub attrs: HashMap<String, Node>,
    pub content: Vec<Node>,
}

pub enum Node {
    Element(ElementNode),
    Text(String),
}

pub type AttributeNodeTree = ElementNode;

Remember that Box<…> is required in rust to give the data structure a finite size.

Conclusion

I think these definitions are helpful to distinguish various cases. But here comes the important question:

What I defined here is nothing new. I only attached names to existing concepts. So why is there no unified framework to operate on these kinds of trees? I am thinking about the capability to extract information from these trees by referring to a node. I am thinking about the capability to rearrange elements from one tree structure to another. Obviously, for XML trees this exists in form of the XSLT and XPath specifications, but why are the tools not more established? Why can I not extract the tree from one document, have some generic framework available to apply operations and then serialize it to such structure again?

We need more tool support for structure trees, content trees, XML trees and attribute-node trees.