Motivation
Classic McEliece (Wikipedia) is a coding-based post-quantum cryptographic scheme. It implements a key encapsulation mechanism using Binary Goppa codes. It is considered a conservative choice, because the basis of the scheme was proposed in 1978; 43 years ago (“A Public-Key Cryptosystem Based On Algebraic Coding Theory” by Robert McEliece).
One interesting part is the uint64_sort function, which seems to sort integers with an algorithm unknown to me.
Source code
#include <inttypes.h>
#include <stdio.h>
#define uint64_MINMAX(a,b) \
do { \
uint64_t c = b - a; \
c >>= 63; \
c = -c; \
c &= a ^ b; \
a ^= c; \
b ^= c; \
} while(0)
static void uint64_sort(uint64_t *x,long long n)
{
long long top,p,q,r,i;
if (n < 2) return;
top = 1;
while (top < n - top) top += top;
for (p = top;p > 0;p >>= 1) {
for (i = 0;i < n - p;++i)
if (!(i & p))
uint64_MINMAX(x[i],x[i+p]);
i = 0;
for (q = top;q > p;q >>= 1) {
for (;i < n - q;++i) {
if (!(i & p)) {
uint64_t a = x[i + p];
for (r = q;r > p;r >>= 1)
uint64_MINMAX(a,x[i+r]);
x[i + p] = a;
}
}
}
}
}An example call
// ASSUME n > 1
void print_array(uint64_t *arr, long long n)
{
printf(" array = %lu", arr[0]);
for (int i = 1; i < n; i++)
printf(", %lu", arr[i]);
printf("\n");
}
void example()
{
uint64_t tmp[42];
// initialize with generated values
for (int i = 0; i < 42; i++)
tmp[i] = (2049 * i + 2) % 49;
// print before
printf("before:\n");
print_array(tmp, 42);
// sort algorithm
uint64_sort((uint64_t*) tmp, 42);
// print after
printf("after:\n");
print_array(tmp, 42);
}This actually sorts the array:
before:
array = 2, 42, 33, 24, 15, 6, 46, 37, 28, 19, 10, 1, 41, 32, 23, 14, 5, 45, 36, 27, 18, 9, 0, 40, 31, 22, 13, 4, 44, 35, 26, 17, 8, 48, 39, 30, 21, 12, 3, 43, 34, 25
after:
array = 0, 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 13, 14, 15, 17, 18, 19, 21, 22, 23, 24, 25, 26, 27, 28, 30, 31, 32, 33, 34, 35, 36, 37, 39, 40, 41, 42, 43, 44, 45, 46, 48Conditional swap
Macro uint64_MINMAX might seem unreadable, but it can be described with a simple property: conditional swap.
If a ≤ b, the values are retained. If a > b, the values are swapped.
Ignoring the macro hygiene syntax (do…while, local variable), one recognizes that b - a computes the difference between the two arguments. If b < a, then computing c means handling an underflow. As a result, the 64th bit of c will be set.
|
Note
|
Actually, this implicitly assumes that \(a, b \in \{0, 1, \dots, 2^{63}-1\}\), because \((2^{64}-1) - (0) = 2^{64}-1\) has the 64th bit set of c, but a > b. (I would love to see such assumptions documented in code per default).
|
With this assumption and the right-shift by 63 positions, c is 1 (if \(b \leq a\)) or c is 0 (if \(b > a\)). With c = -c, we get either an integer with all bits set (if \(b \leq a\)) or c is 0 (if \(b > a\)).
If we get 0, it will obviously lead to no change in the three assignments. However, if all bits are set, we get …
… which represents a swap. As a result with \(a, b \in \{0, 1, \dots, 2^{63}-1\}\), we get \(a', b' = \operatorname{uint64\_MINMAX}(a, b)\) which satisfies \(a' \leq b'\).
void cond_swap()
{
uint64_t g = 1, h = 42;
uint64_MINMAX(g, h);
printf("%d\n", g <= h); // is "1"
uint64_t i = 33, j = 12;
uint64_MINMAX(i, j);
printf("%d\n", i <= j); // is "1"
uint64_t k = 11, l = 11;
uint64_MINMAX(k, l);
printf("%d\n", k <= l); // is "1"
}Why the complexity and not a simple if-statement? Because the algorithm shall run in constant time to avoid side channel leakage (timing or power consumption must not correlate with the value).
Understanding top
The first step of uint64_sort is to evaluate top based on the value of n. We can create a table …
| n | top | n | top | n | top | n | top | n | top | n | top | n | top | n | top | n | top |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
2 |
1 |
3 |
2 |
4 |
2 |
5 |
4 |
6 |
4 |
7 |
4 |
8 |
4 |
9 |
8 |
10 |
8 |
11 |
8 |
12 |
8 |
13 |
8 |
14 |
8 |
15 |
8 |
16 |
8 |
17 |
16 |
18 |
16 |
19 |
16 |
20 |
16 |
21 |
16 |
22 |
16 |
23 |
16 |
24 |
16 |
25 |
16 |
26 |
16 |
27 |
16 |
28 |
16 |
29 |
16 |
30 |
16 |
31 |
16 |
32 |
16 |
33 |
32 |
34 |
32 |
35 |
32 |
36 |
32 |
37 |
32 |
38 |
32 |
39 |
32 |
40 |
32 |
41 |
32 |
42 |
32 |
43 |
32 |
44 |
32 |
45 |
32 |
46 |
32 |
47 |
32 |
48 |
32 |
49 |
32 |
50 |
32 |
51 |
32 |
52 |
32 |
53 |
32 |
54 |
32 |
55 |
32 |
56 |
32 |
57 |
32 |
58 |
32 |
59 |
32 |
60 |
32 |
61 |
32 |
62 |
32 |
63 |
32 |
64 |
32 |
Apparently, top is defined as largest power-of-two smaller than n.
Understanding nested loops
The next loops of the algorithm are pretty intricate.
Loop i
for (p = top;p > 0;p >>= 1) {
for (i = 0;i < n - p;++i)
if (!(i & p))
uint64_MINMAX(x[i],x[i+p]);
}-
Let
nbe ∈ {5, 6, 7, 8}, thentopequals 4. Thus the looppgoes 4 → 2 → 1 → 0. -
Let
nbe ∈ {9, 10, …, 16}, thentopequals 8. Thus the looppgoes 8 → 4 → 2 → 1 → 0. -
Essentially,
pwalks down powers-of-two. It satisfies the property that only one bit is set.
Thus, p decreases logarithmically.
Let us write a small routine, which dumps the loop variables:
for (p = top;p > 0;p >>= 1) {
printf("p = %llu\n", p);
for (i = 0;i < n - p;++i) {
printf(" i = %llu", i);
if (!(i & p)) {
printf(" → swap conditionally x[%llu] and x[%llu]", i, i+p);
}
printf("\n");
}
}… which (for n=7) gives us …
p = 4
i = 0 → swap conditionally x[0] and x[4]
i = 1 → swap conditionally x[1] and x[5]
i = 2 → swap conditionally x[2] and x[6]
p = 2
i = 0 → swap conditionally x[0] and x[2]
i = 1 → swap conditionally x[1] and x[3]
i = 2
i = 3
i = 4 → swap conditionally x[4] and x[6]
p = 1
i = 0 → swap conditionally x[0] and x[1]
i = 1
i = 2 → swap conditionally x[2] and x[3]
i = 3
i = 4 → swap conditionally x[4] and x[5]
i = 5I would rename p as a window_size. It defines the size of a window, which is used to conditionally swap the first elements of windows. We ensure x[0] ≤ x[4], x[1] ≤ x[5], and x[2] ≤ x[6]. Does this sort the elements x[0] to x[6]? No, because only two elements satisfy the property, but not all of them. As a result, we also need to halve the window size and run the algorithm there. Since (e.g.) x[0] ≤ x[4], x[0] ≤ x[2], as well as x[0] ≤ x[1], we satisfy x[0] ≤ x[1] ≤ x[2] ≤ x[4]. If we consider all indices, we get x[0] ≤ x[1] ≤ … ≤ x[6].
-
The condition
i < n - pmakes sure we stop, before we get out of bounds withx[n](recognize that we use maximum indexi+p). -
The condition
!(i & p)makes sure, we don’t conditionally swap elements which are ordered by the logarithmic structure anyways. Why does the AND operation work here? Because we conditionally swapped elements with indexiandi+p, we want to skip alliwhich occured as indexi+pbefore. Those indices are given byi & pbecause allpare powers-of-two.
Loop q
The final part TODO
for (p = top;p > 0;p >>= 1) {
i = 0;
for (q = top;q > p;q >>= 1) {
for (;i < n - q;++i) {
if (!(i & p)) {
uint64_t a = x[i + p];
for (r = q;r > p;r >>= 1)
uint64_MINMAX(a,x[i+r]);
x[i + p] = a;
}
}
}
}Once more, vet us write a small routine, which dumps the loop variables:
for (p = top;p > 0;p >>= 1) {
printf("p = %llu\n", p);
for (i = 0;i < n - p;++i) {
printf(" i = %llu", i);
if (!(i & p)) {
printf(" → swap conditionally x[%llu] and x[%llu]", i, i+p);
}
printf("\n");
}
i = 0;
for (q = top;q > p;q >>= 1) {
printf(" q = %llu\n", q);
for (;i < n - q;++i) {
printf(" i = %llu", i);
if (!(i & p)) {
printf(" → loop conditionally\n");
printf(" a = x[%llu]\n", i + p);
for (r = q;r > p;r >>= 1)
{
printf(" r = %llu → swap conditionally a and x[%llu]\n", r, i+r);
}
printf(" x[%llu] = a", i + p);
}
printf("\n");
}
}
}This is an informal description, which gave me an intuition why this algorithm works. But how about a proof?
Tracing the origins
Bernhard pointed me to literature by Daniel J. Bernstein. Indeed, he lead a research project on sorting algorithms. In the context of cryptography we are looking for the fastest sorting algorithm whose runtime can depend on the number of elements but must not depend on the content of the elements (due to side-channel security).
-
At sorting.cr.yp.to, djbsort is a sorting algorithm built upon older theory. Indeed current release djbsort-20190516 file
/h-internal/int32_minmax.cshows the macro we discussed. An assembly-optimized version for x86 is provided as well. File/int32/portable3/sort.cshows the algorithm, we discuss. -
Looking further, we find that some literature contains the algorithm. I found “NTRU Prime: reducing attack surface at low cost” by Bernstein, Chuengsatiansup, Lange, and Vredendaal (recognize that Bernstein and Lange are submitters of both schemes, “NTRU Prime” as well as “Classic McEliece”). Figure S.1 at page 49 shows the algorithm.
-
A sorting network accesses elements for conditional swaps in a structured manner which usually makes it well-suited for vectorization (parallelization on instruction level). Since, we need to always access elements in the same way (independent of the element values), sorting networks are certainly a good choice.
-
Looking up notes in the NTRU prime paper, this algorithm is djbsort which is based on Batcher’s sorting network (1968).
The original release of djbsort happened in 2018:
First release of djbsort: super-fast constant-time automatically verified AVX2 sorting code for int32 arrays. https://sorting.cr.yp.to (Next target is ARM NEON.) Verification starts with the #angr toolkit for symbolic execution, which in turn uses libVEX from Valgrind. [tweet]
We use the classic “odd-even merging network” introduced by Batcher [13] in 1968. Figure S.1 is a C translation of Knuth’s “merge exchange” in [75, Algorithm 5.2.2M], a simplified presentation of Batcher’s odd-even merging network. Beware that many other descriptions of Batcher’s method require n to be a power of 2.
To understand the vectorizability of this sorting network, consider the first i loop in Figure S.1 for n = 761. The top variable is set to 512, and the p variable starts at 512. The i loop compares x[0] with x[512], compares x[1] with x[513], etc., and finally compares x[248] with x[760]. To vectorize this we simply pick up x[0] through x[7] as a vector, pick up x[512] through x[519] as a vector, perform vector min and max operations, etc.
Later in the computation, when p is small, the vectorization becomes somewhat more intricate, requiring some permutations of vector entries.
Discovering the theory behind sorting networks
In The Art Of Computer Programming (Volume 3, 2nd edition), we find the following statements:
In this section, we shall discuss four types of sorting methods for which exchanging is a dominant characteristic: exchange selection (the “bubble sort”); merge exchange (Batcher’s parallel sort); partition exchange (Hoare’s “quicksort”); and radix exchange.
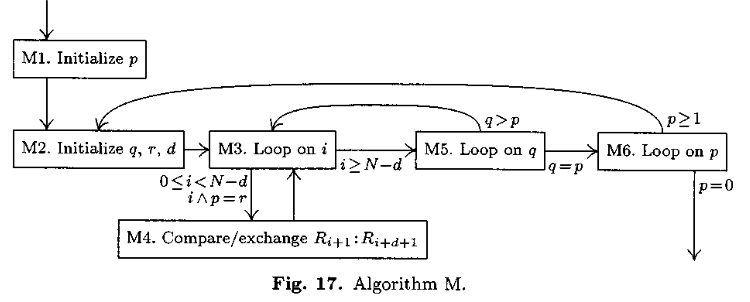
Algorithm M (Merge exchange). Records R₁, …, Rₙ are rearranged in place; after sorting is complete their keys will be in order, K₁, …, Kₙ. We assume that n ≥ 2.
[Initialize p.] Set p ← 2t-1, where t = ⌈lg n⌉ is the least integer such that 2t ≥ n. (Steps M2 through M5 will be performed for p = 2t-1, 2t-2, …, 1.)
[Initialize p, r, d.] Set q ← 2t-1, r ← 0, d ← p.
[Loop on i.] For all i such that 0 ≤ i ≤ n - d and i & p = r, do step 4. Then go to step 5. (Here i & p means the “bitwise and” of the binary representations of i and p, each bit of the result is zero except where both i and p have 1-bits in corresponding positions. Thus 13 & 21 = (1101)2 & (10101)2 = (00101)2 = 5. At this point, d is an odd multiple of p, and p is a power of 2, so that i & p ≠ (i + d) & p; it follows that the actions of step 4 can be done for all relevant i in any order, even simultaneously.)
[Compare/exchange Ri+1:Ri+d+1.] If Ki+1 > Ki+d+1 interchange the records Ri+1 ⟷ Ri+d+1.
[Loop on q.] If q ≠ p, set d ← q - p, q ← q/2, r ← p, and return to step 3.
[Loop on p.] (At this point the permutation K₁ K₂ … Kn is p-ordered.) Set p ← ⌊p/2⌋. If p > 0, go back to step 2.
Section 5.3.4